Решение задач геометрической прогрессии

Основные понятия и определения.

Геометрической прогрессией  называется числовая последовательность следующего вида:

где каждый член , начиная со второго, равен произведению предыдущего  члена и числа   , так называемого знаменателя геометрической прогрессии, а первый член прогрессии имеет конкретное значение.

Для наглядности можно привести следующие примеры геометрической прогрессии:

а) Это геометрическая прогрессия, у которой

б)  Это геометрическая прогрессия, у которой

в)  Это геометрическая прогрессия, у которой

г)  Это геометрическая прогрессия, у которой

Можно заметить, что если и , то геометрическая прогрессия возрастающая. А если и , то геометрическая прогрессия убывающая.

Если отбросить все члены геометрической прогрессии, которые следуют за выбранным конкретным числом, то она станет конечной.

Для вычисления n-ого члена геометрической прогрессии  используется следующая формула:

Необходимо знать, что  квадрат каждого члена геометрической прогрессии (кроме первого и последнего) равен произведению предшествующего и последующего членов этой прогрессии (характеристическое свойство геометрической прогрессии):

Для вычисления суммы n членов конечной геометрической прогрессии используется формула:

Для вычисления суммы членов бесконечно убывающей геометрической прогрессии используется формула:

Пример 1: Составить формулу n-ого члена числовой последовательности

Легко заметить, что данная числовая последовательность является геометрической прогрессией, у которой

Составим формулу n-ого члена:

Ответ:

Пример 2: Составить формулу n-ого члена числовой последовательности

Легко заметить, что данная числовая последовательность является геометрической прогрессией, у которой

Составим формулу n-ого члена:

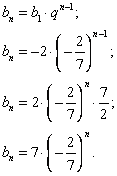
Ответ:

Пример 3: Составить формулу n-ого члена числовой последовательности

Легко заметить, что данная числовая последовательность является геометрической прогрессией, у которой

Составим формулу n-ого члена:

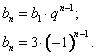
Ответ:

Пример 4: Дана геометрическая прогрессия

а) Известно, что . Найти .

б) Известно, что . Найти .

в) Известно, что . Найти .

г) Известно, что . Найти .

Во всех случаях в основе будет лежать формула для вычисления n-ого члена геометрической прогрессии:

а) Так как необходимо найти пятый член геометрической прогрессии, то мы имеем следующие условия: .

Воспользуемся вышеприведенной формулой:

б) Так как известно, что .

Найдем , используя вышеприведенную формулу:

в) Так как задан пятый член геометрической прогрессии, то мы имеем следующие условия: .

Найдем , используя вышеприведенную формулу:

г) Так как задан первый и восьмой член геометрической прогрессии, то мы имеем следующие условия: .

Найдем , используя вышеприведенную формулу:

Ответ: а) б) в)  г)

Пример 5: Между числами 2 и 18 вставьте три числа так, чтобы получилась геометрическая прогрессия.

 По условию задачи имеем:   Нужно найти . Составим формулу для пятого члена геометрической прогрессии, используя формулу вычисления n-ого члена:

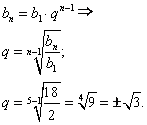
Тогда, если, то имеем следующие члены геометрической прогрессии:

А если, то имеем следующие члены геометрической прогрессии:

Ответ: или

Пример 6: Фигура составляется из квадратиков так, как показано на рисунке. В каждом следующем ряду в 2 раза квадратов больше, чем в предыдущем. Сколько квадратов в 17 ряду?

Легко заметить, что данную задачу можно решить, опираясь на понятия геометрической прогрессии, у которой  так как в первом ряду фигуры четыре квадрата, а так как в каждом последующем ряду квадратов в 2 раза больше, чем в предыдущем.

Опираясь на полученные выводы, найдем :

Примечание: На примере данной задачи видно, что не целесообразно рисовать семнадцать рядов фигуры и считать количество квадратов в нем, как делают многие ученики, что ведет к большому числу ошибок. Гораздо разумнее увидеть, что задача сводится к нахождению n-ого члена геометрической прогрессии.

Ответ:

Пример 7: Разность между седьмым и пятым членами геометрической прогрессии равна 96, сумма пятого и шестого членов прогрессии равна 96. Найти пятнадцатый член этой прогрессии.

По условию задачи имеем:  Составим формулы для пятого, шестого и седьмого члена, используя формулу вычисления n-ого члена  геометрической прогрессии:

Подставим полученные формулы в записанное нами ранее условие задачи:

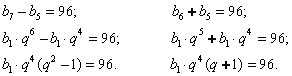
Составим систему уравнений и решим ее:

Подставив значение  во второе уравнение системы, получим , то есть .

Подставив значение  во второе уравнение системы, получим , то есть уравнение не имеет решений.

Таким образом, мы имеем геометрическую прогрессию, у которой .

Так как необходимо найти пятнадцатый член этой прогрессии, воспользуемся формулой вычисления n-ого члена  геометрической прогрессии:

Ответ:

Пример 8: Дана конечная геометрическая прогрессия

а) Известно, что . Найти сумму .

б) Известно, что. Найти .

Во всех случаях в основе будет лежать формула для вычисления суммы n членов конечной геометрической прогрессии:

а) Так как известно, что

Воспользуемся вышеприведенной формулой:

б) Так как известно, что.

Воспользуемся формулой вычисления n-ого члена  геометрической прогрессии:

Используем вышеприведенную формулу суммы:

Так как ранее мы получили, что , то имеем:

Ответ: а) б)

Пример 9: Дана бесконечно убывающая геометрическая прогрессия  Известно, что . Найти сумму .

В основе будет лежать формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии:

Ответ:

Пример 10: Найти сумму первых восьми членов геометрической прогрессии, у которой второй член равен 6, а четвертый равен 24.

Воспользуемся формулой вычисления n-ого члена  геометрической прогрессии и выразим второй и четвертый члены:

Так как по условию второй и четвертый члены геометрической прогрессии равны 6 и 24 соответственно, то составим систему уравнений:

Поделим второе уравнение системы на первое и получим:

Подставив значение  в первое уравнение системы, получим , то есть .

Подставив значение  в первое уравнение системы, получим , то есть .

В основе будет лежать формула для вычисления суммы n членов конечной геометрической прогрессии:

Если  и , то сумма первых восьми членов геометрической прогрессии будет вычислена следующим образом:

Если  и , то сумма первых восьми членов геометрической прогрессии будет вычислена следующим образом:

Ответ:  или

Пример 11: При каких значениях  числа ,  и  образуют конечную геометрическую прогрессию?

Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению:

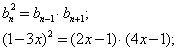
Решим это уравнение:

При этом значении заданные выражения принимают соответственно значения . Это геометрическая прогрессия, у которой  

Ответ:

Автор статьи: Каташева Г.Г.