При исследовании заданной функции y=f(x) и построении ее графика необходимо руководствоваться следующим алгоритмом:

Исследование функции y=f(x) по ее внешнему виду.

1. Найти область определения  функции.
2. Исследовать функцию на четность/нечетность.
3. Найти точки пересечения графика функции с осями координат (так называемые нули функции).
4. Найти  точки разрыва функции и определить их характер.
5. Найти асимптоты графика функции.

5*. Если функция содержит тригонометрические компоненты, необходимо исследовать ее периодичность.

Исследование функции y=f(x) по первой производной.

1. Определить интервалы возрастания, убывания и экстремумы функции.

Исследование функции y=f(x) по второй производной.

1. Определить интервалы выпуклости, вогнутости и точки перегиба графика функции, найти значения функции в точках перегиба.

Построение графика функции y=f(x).

1. Нанести на координатную плоскость характерные точки и, используя полученные результаты исследования функции, построить ее график. Если внешний вид графика после исследования трудно определить, то необходимо взять несколько контрольных точек.

Замечание. Область определения функции необходимо искать, используя известные свойства элементарных функций, например следующие:

1. Функция  не определена при значениях аргумента x, при которых g(x)=0.
2. Корни четной степени (  и т.д.) определены только при неотрицательных значениях подкоренного выражения ().
3. Логарифмическая функция  определена только при положительных значениях x (x>0).
4. Функции  y=arcsin x и y=arcos x  определены только при .

Типовые примеры решения задачи исследования функции и построения ее графика.

Пример 1: Исследовать функцию  и построить ее график.

1. Функция   определена для всех . (см. замечания к алгоритму исследования).
2. Найдем y(-x): данная функция не является ни четной, ни нечетной.
3. Найдем точки пересечения графика функции с осями координат:

Если , то , то есть график функции пересекает ось Оy в точке А(0,-4).

Если , тогда из уравнения  найдем . То есть график функции пересекает ось Ох в точках В(1,0), С(-2,0).

1. Заданная функция непрерывна во всех точках числовой оси как многочлен третьей степени.
2. График функции не имеет вертикальных асимптот, так как заданная функция непрерывна на всей числовой оси.

График функции не имеет горизонтальных асимптот, так как:

Определим, имеет ли график функции наклонные асимптоты:

Следовательно, угловой коэффициент наклонной асимптоты не является конечным и график функции таковой асимптоты не имеет.

1. Исследуем заданную функцию на возрастание, убывание и экстремумы.

Найдем первую производную:

Приравняем производную к нулю и решим полученное уравнение:

Найдем промежутки знакопостоянства первой производной:

Таким образом, функция :

- возрастает на интервалах

- убывает на интервале

- в точке  имеет максимум ();

- в точке  имеет минимум ().

1. Определим интервалы выпуклости, вогнутости и точки перегиба графика функции.

Найдем вторую производную:

Приравняем производную к нулю и решим полученное уравнение:

Найдем промежутки знакопостоянства второй производной:

Таким образом кривая:

- выпукла на интервале

- вогнута на интервале

Точка  - точка перегиба ().

1. Нанесем на координатную плоскость характерные точки и, используя полученные результаты исследования функции, построим ее график.

Замечание. Для удобства построения можно объединить полученные результаты в таблицу:

Рис.1: График функции .

Пример 2: Исследовать функцию  и построить ее график.

1. Функция   определена при всех значениях, то есть . (см. замечания к алгоритму исследования).
2. Найдем y(-x): данная функция является нечетной и  график функции будет симметричен относительно начала координат.
3. Найдем точки пересечения графика функции с осями координат:

Если , то ,если , то . Следовательно, график функции проходит через начало координат O(0,0).

1. Найдем точки разрыва и определим их характер.

Функция не определена при . Исследуем поведение функции вблизи точек разрыва :

Следовательно, - точки разрыва второго рода.

1. Прямые - двусторонние вертикальные асимптоты. (см. п. 4 данного исследования).

График функции не имеет горизонтальных асимптот, так как:

Определим, имеет ли график функции наклонные асимптоты:

Следовательно, k=1, b=0 и прямая y = x (y = kx+b) является наклонной асимптотой графика функции.

1. Исследуем заданную функцию на возрастание, убывание и экстремумы.

Найдем первую производную:

Приравняем производную к нулю и решим полученное уравнение:

Найдем промежутки знакопостоянства первой производной:

Таким образом, функция :

- возрастает на интервалах

- убывает на интервалах

- в точке  имеет максимум ();

- в точке  имеет минимум ().

1. Определим интервалы выпуклости, вогнутости и точки перегиба графика функции.

Найдем вторую производную:

Приравняем производную к нулю и решим полученное уравнение:

Найдем промежутки знакопостоянства второй производной:

Таким образом кривая:

- выпукла на интервалах

- вогнута на интервалах

Точка  - точка перегиба ().

1. Нанесем на координатную плоскость характерные точки и, используя полученные результаты исследования функции, построим ее график.

Объединим полученные результаты в таблицу:

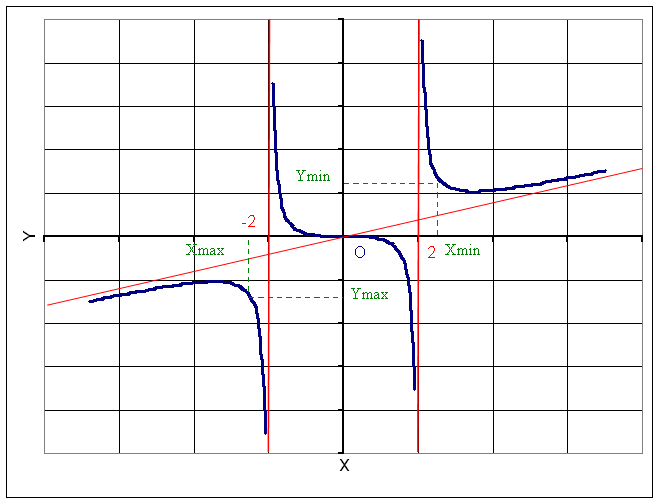
Рис.2: График функции .

Пример 3: Исследовать функцию  и построить ее график.

1. Функция   определена при положительных значениях, то есть . (см. замечания к алгоритму исследования).
2. -
3. Найдем точки пересечения графика функции с осью Ох, т.к.  не входит в область определения функции и точек пересечения с осью  Оy не будет:

Если , тогда из уравнения  найдем . То есть график функции пересекает ось Ох в точке В(1,0).

1. В области определения функция является непрерывной, как произведение непрерывных функций.
2. Так как заданная функция является непрерывной, то вертикальных асимптот нет.

Исследуем поведение функции вблизи граничной точки :

При исследовании применялось правило Лопиталя.

График функции не имеет горизонтальных асимптот, так как:

Определим, имеет ли график функции наклонные асимптоты:

Следовательно, угловой коэффициент наклонной асимптоты не является конечным и график функции таковой асимптоты не имеет.

1. Исследуем заданную функцию на возрастание, убывание и экстремумы.

Найдем первую производную:

Приравняем производную к нулю и решим полученное уравнение:

Найдем промежутки знакопостоянства первой производной:

Таким образом, функция :

- возрастает на интервале

- убывает на интервале

- в точке  имеет минимум

1. Определим интервалы выпуклости, вогнутости и точки перегиба графика функции.

Найдем вторую производную:

Приравняем производную к нулю и решим полученное уравнение:

Найдем промежутки знакопостоянства второй производной:

Таким образом кривая:

- выпукла на интервале

- вогнута на интервале

Точка  - точка перегиба .

1. Нанесем на координатную плоскость характерные точки и, используя полученные результаты исследования функции, построим ее график.

Объединим полученные результаты в таблицу:

 Стрелка на графике показывает, что точка не входит в область определения функции и имеет конечный предел

Рис.3: График функции.

Пример 4: Исследовать функцию  и построить ее график.

1. Функция   определена для всех . (см. замечания к алгоритму исследования).
2. Найдем y(-x): данная функция является четной и  график функции будет симметричен относительно оси Оу.
3. Найдем точки пересечения графика функции с осями координат:

Если , то , то есть график функции пересекает ось Оy в точке А(0,3).

Если , тогда из уравнения  найдем . То есть график функции пересекает ось Ох в точках

.

1. Заданная функция непрерывна во всех точках числовой оси как многочлен четвертой степени.
2. График функции не имеет вертикальных асимптот, так как заданная функция непрерывна на всей числовой оси.

График функции не имеет горизонтальных асимптот, так как:

Определим, имеет ли график функции наклонные асимптоты:

Следовательно, угловой коэффициент наклонной асимптоты не является конечным и график функции таковой асимптоты не имеет.

1. Исследуем заданную функцию на возрастание, убывание и экстремумы.

Найдем первую производную:

Приравняем производную к нулю и решим полученное уравнение:

Найдем промежутки знакопостоянства первой производной:

Таким образом, функция :

- возрастает на интервалах

- убывает на интервалах

- в точке  имеет максимум ();

- в точках  имеет минимум .

1. Определим интервалы выпуклости, вогнутости и точки перегиба графика функции.

Найдем вторую производную:

Приравняем производную к нулю и решим полученное уравнение:

Найдем промежутки знакопостоянства второй производной:

Таким образом кривая:

- выпукла на интервале

- вогнута на интервалах

Точки  - точки перегиба .

1. Нанесем на координатную плоскость характерные точки и, используя полученные результаты исследования функции, построим ее график.

              Рис.4: График функции.