Площадь трапеции
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
| при известных длинах оснований и высоты. |
| при известных длинах высоты и средней линии. |
| при известных длинах оснований и боковых сторон. |
| Вычисление площади равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании. |
Общая теория для вычисления площади трапеции.
Трапеция – это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.
Две параллельные стороны трапеции называются основаниями трапеции.
Две не параллельные стороны трапеции называются боковыми сторонами трапеции.
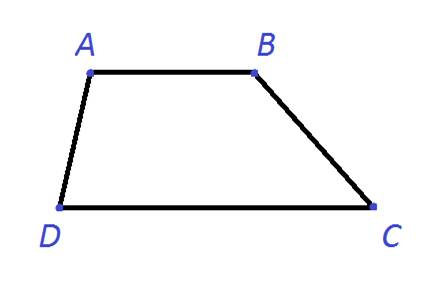
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC – основания трапеции ABCD.
AD, BC – боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
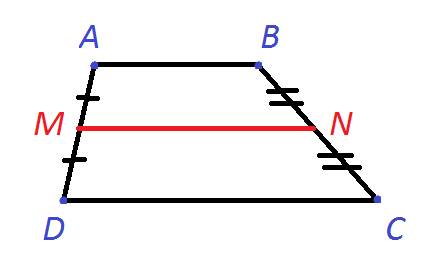
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,![]() .
.
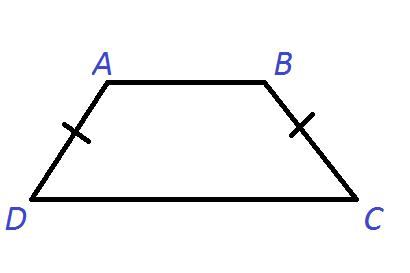
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой), если ее боковые стороны равны.
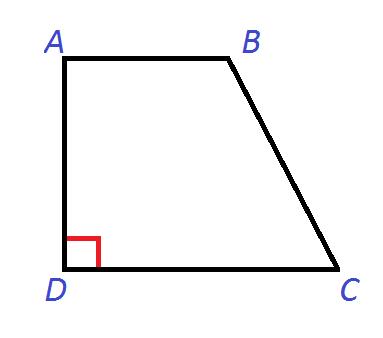
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D – прямой (равен 90о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту: ![]()
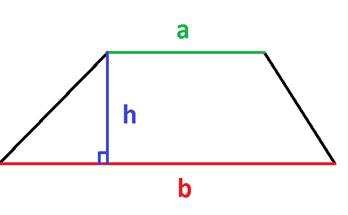
2. Площадь трапеции равна произведению ее средней линии на высоту: ![]()
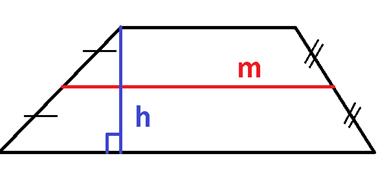
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле: 
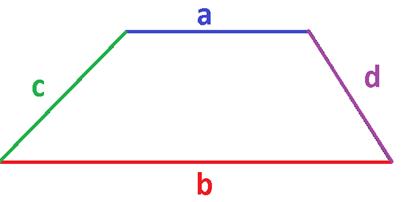
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле: ![]()
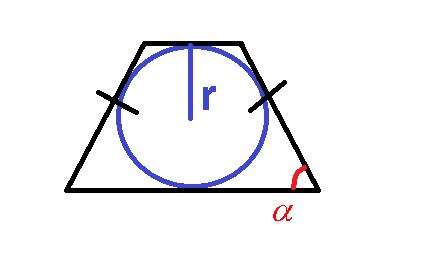
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
![]()
Таким образом, имеем следующее:
![]()
Ответ: ![]()
Пример 2: Найти сторону основания трапеции с площадью S=35 см2, высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
![]()
Выразим из данной формулы сторону основания трапеции:
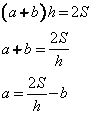
Таким образом, имеем следующее:
![]()
Ответ: ![]()
Пример 3: Найти высоту трапеции с площадью S=17 см2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
![]()
Выразим из данной формулы высоту трапеции:
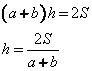
Таким образом, имеем следующее:
![]()
Ответ: ![]()
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
![]()
Таким образом, имеем следующее:
![]()
Ответ: ![]()
Пример 5: Найти высоту трапеции с площадью S = 48 см2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
![]()
Выразим из данной формулы высоту трапеции:
![]()
Таким образом, имеем следующее:
![]()
Ответ: ![]()
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
![]()
Выразим из данной формулы среднюю линию трапеции:
![]()
Таким образом, имеем следующее:
![]()
Ответ: ![]()
Пример 7: Вычислить площадь трапеции с основаниями a=2, b=6 и боковыми сторонами c=3, d=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:

Таким образом, имеем следующее:
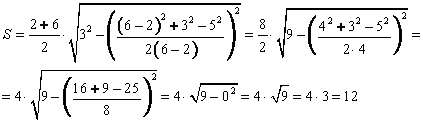
Ответ: ![]()
Пример 8: Вычислить площадь равнобедренной трапеции с радиусом вписанной окружности r=9 и углом при основании трапеции α=30о.
Решение:
Для нахождения площади равнобедренной трапеции воспользуемся следующей формулой вычисления площади:
![]()
Таким образом, имеем следующее:
![]()
Ответ: ![]()
Пример 9: Вычислить радиус вписанной в равнобедренную трапецию окружности, если площадь трапеции S=200 и углом при основании трапеции α=30о.
Решение:
Для нахождения радиуса вписанной в равнобедренную трапецию окружности воспользуемся следующей формулой вычисления площади:
![]()
Выразим из данной формулы радиус:

Таким образом, имеем следующее:
![]()
Ответ: ![]()
Пример 9: Вычислить угол при основании трапеции, считая, что он острый. Если радиус вписанной в равнобедренную трапецию окружности r =![]() и площадь трапеции S=
и площадь трапеции S=![]() .
.
Решение:
Для нахождения угла при основании трапеции воспользуемся следующей формулой вычисления площади:
![]()
Выразим из данной формулы угол при основании трапеции:
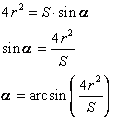
Таким образом, имеем следующее:

Ответ: ![]()