Решение биквадратных уравнений

Биквадратным уравнением называется уравнение следующего вида:

где - любые действительные числа, но , x – неизвестная искомая переменная.

Коэффициенты  имеют соответственно названия: - старший коэффициент (коэффициент при ), - второй коэффициент (коэффициент при ), - свободный член.

Корнем биквадратного уравнения называется такое значение переменной , при подстановке которого трехчлен обращается в ноль.

Решить биквадратное уравнение – это значит найти все его корни или установить, что корней нет.

При решении биквадратного уравнения  необходимо придерживаться следующей схемы:

1)       Подстановкой свести заданное биквадратное уравнение к квадратному уравнению вида

2)       Найти корни полученного квадратного уравнения. (См. схему решения квадратных уравнений).

3)       Приравнять полученные значения корней квадратного уравнения к введенной переменной подстановки . То есть провести обратную замену.

4)       Найти корни биквадратного уравнения, решив уравнения обратной замены.

Пример 1: Решить уравнение

Данное уравнение является биквадратным.

Введем замену переменных:

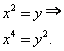
Тогда заданное уравнение перепишется в следующем виде:

Полученное уравнение является полным неприведенным и имеет следующие коэффициенты:

Найдем дискриминант:

Так как , то квадратное уравнение имеет два корня.

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Введем обратную замену  и . И решим полученные уравнения:

Ответ:

Пример 2: Решить уравнение

Данное уравнение является биквадратным.

Введем замену переменных:

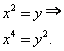
Тогда заданное уравнение перепишется в следующем виде:

Полученное уравнение является полным приведенным и имеет следующие коэффициенты:

Найдем дискриминант:

Так как , то квадратное уравнение имеет два корня.

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Введем обратную замену  и . И решим полученные уравнения:

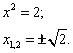
Уравнение же  решения не имеет.

Таким образом, решением биквадратного уравнения будут корни

Ответ:

Примечание: Из решенного выше примера видно, что при получении отрицательного значения корня квадратного уравнения , можно сразу исключать его из рассмотрения как неудовлетворяющего условию

Пример 3: Решить уравнение

Данное уравнение является биквадратным.

Введем замену переменных:

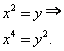
Тогда заданное уравнение перепишется в следующем виде:

Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .

Найдем дискриминант: .

Так как , то квадратное уравнение не имеет корней.

Таким образом, биквадратное уравнение тоже не имеет корней.

Ответ:  Корней нет.

Пример 4: Решить уравнение

Данное уравнение является биквадратным.

Введем замену переменных:

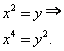
Тогда заданное уравнение перепишется в следующем виде:

Полученное уравнение является полным приведенным и имеет следующие коэффициенты:

Найдем дискриминант:

Так как , то квадратное уравнение имеет два корня.

Найдем их:

Таким образом, решением квадратного уравнения будут корни

Так как оба полученных корня квадратного уравнения отрицательны , то биквадратное уравнение иметь решений не будет. (Смотри примечание данной главы)

Ответ: Корней нет.

Автор статьи: Каташева Г.Г.