Решение двучленных уравнений четвертой степени

Двучленными уравнениями четвертой степени называются уравнения вида:  

 или

где - любые действительные числа, но , x – неизвестная искомая переменная.

Корнем двучленного уравнения четвертой степени называется такое значение переменной , при подстановке которого двучлен  или  обращается в ноль.

Решить  уравнение – это значит найти все его корни или установить, что корней нет.

При решении двучленного уравнения вида необходимо придерживаться следующей схемы:

1)      Вынести за скобки общий множитель , преобразовав тем самым заданное уравнение к виду

2)      Решить полученное уравнение, приравняв каждый множитель к нулю:

Пример 1: Решить уравнение

Данное уравнение является двучленным уравнением четвертой степени.

Вынесем за скобки общий множитель :

Поэтому либо , либо

Ответ:

Пример 2: Решить уравнение

Данное уравнение является двучленным уравнением четвертой степени.

Вынесем за скобки общий множитель :

Поэтому , либо

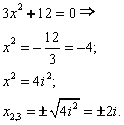
Таким образом, заданное уравнение имеет три решения.

Ответ:

При решении двучленного уравнения вида  при необходимо придерживаться следующей схемы:

1)      Привести уравнение к виду

2)      Решить полученное уравнение:

Пример 3: Решить уравнение

Данное уравнение является двучленным уравнением четвертой степени.

Решим данное уравнение по вышеприведенной формуле:

Таким образом, заданное уравнение имеет одно решение

Ответ:

При решении двучленного уравнения вида  при  необходимо придерживаться следующей схемы:

1)      Разделить оба члена уравнения на коэффициент при . При этом заданное уравнение примет вид:

2)      Тождественно преобразуем полученное уравнение, прибавив  и вычтя :

3)      Используя формулу сокращенного умножения , привести уравнение к виду:

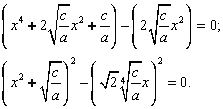
4)      Используя формулу сокращенного умножения , привести уравнение к виду:

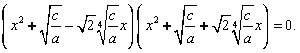
5)      Решить квадратные уравнения  и  

Пример 4: Решить уравнение

Данное уравнение является двучленным уравнением четвертой степени.

Разделим оба члена уравнения на коэффициент :

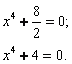
Тождественно преобразуем полученное уравнение согласно вышеприведенной схеме решения, рассчитав

Используя формулу сокращенного умножения , приведем уравнение к виду:

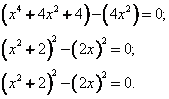
Используя формулу сокращенного умножения , приведем уравнение к виду:

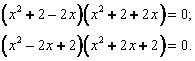
Решим квадратное уравнение

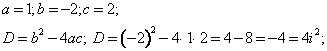
Найдем корни квадратного уравнения:

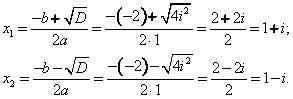
Решим квадратное уравнение

Найдем корни квадратного уравнения:

Таким образом, заданное уравнение имеет четыре решения.

Ответ: